Углы треугольника бывают внутренние и внешние.
Интерактивная модель
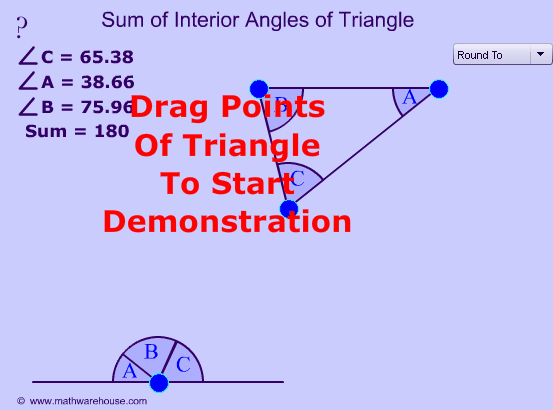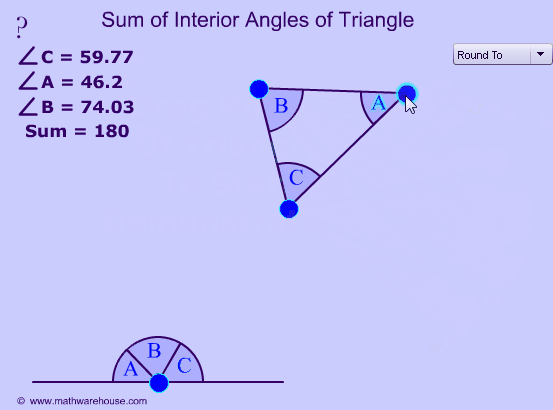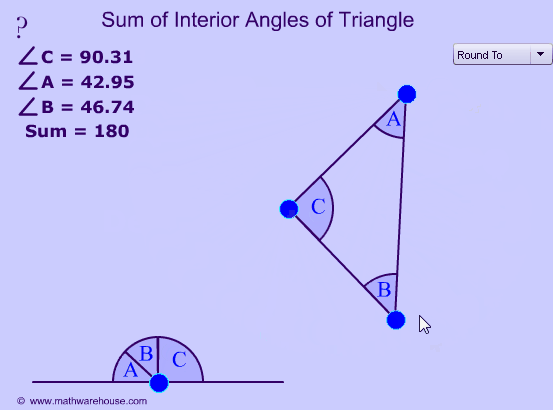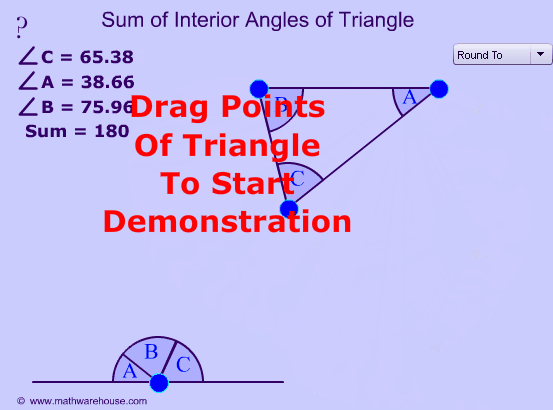
Убедиться в справедливости этой теоремы можно с помощью интерактивной модели
Внутренние углы треугольника - это углы, образованные парами сторон.
Попробуй поработать с моделью и догадаться, чему равна сумма внутренних углов треугольника
Легко доказать, что в сумме эти углы равны 180°, то есть, если их вершины совместить, то получится развернутый угол.
Для доказательства этого факта нам понадобится параллельная прямая
Нарисуем треугольник, а затем проведем прямую из его вершины, параллельную стороне.
Посмотри доказательство на подвижном чертеже |
По свойству углов при параллельных прямых и секущей следует, что соответственные углы равны, накрест лежащие углы равны. Получилось, что углы a, b и с в сумме дают 180°. |
С помощью интерактивной модели, ссылка на которую расположена ниже, вы можете убедиться в справедливости доказанного утверждения. Перемещайте вершины треугольника и наблюдайте за величиной суммы внутренних углов треугольника. Убедитесь в том, что она всегда остается равной 180°.
Внешний угол треугольника при данной вершине — это угол, смежный с внутренним углом треугольника при этой вершине. Чтобы получить внешний угол надо продолжить любую сторону треугольника. Так Ð1 внешний угол при вершине С, а углы 2 и 3 - внешние углы при вершине В. Вообще говоря, у треугольника 6 внешних углов: по два при каждой вершине, но, поскольку они равны, как вертикальные углы, то говоря о внешнем угле можно выбирать любой из них
Убедиться в справедливости этой теоремы можно с помощью интерактивной модели
А теперь попробуйте испытать свои силы, выполняя интерактивное задание, вычисляя углы треугольника






Комментариев нет:
Отправить комментарий