Деление с крокодилами, совсем не страшно

  Быстро выполнять действие деления вам поможет этот веселый тренажер. Выбирайте нужный уровень, необходимую скорость и выбирайте правильный ответ. Надеюсь. что после вашей работы зубы крокодилов станут чистыми и острыми. Вперед!

Учим таблицу производных

     Игра-тренажер "Убей червяка" поможет выучить таблицу производных. Нажимайте молоточком правильный ответ и постарайтесь не делать ошибок. Когда поймете, что все хорошо запомнили, пройдите контроль. Удачи!

Таблица умножения за одну минуту

 

 Всего одна минута дается вам, чтобы проверить знание таблицы умножения. Постарайтесь решить как можно больше примеров. Переходите с одного уровня на другой. Соревнуйтесь с друзьями и становитесь чемпионом!

В паутине. Вычисляем углы.

                 Если вы не хотите напрасно потратить время сидя у компьютера, то можете поиграть в эту математическую игру. В ней вам предстоит с помощью стрелок управлять крошечным роботом-пауком по имени Итзи, который со своей семьей живет в старых дедовских часах. На каждом уровне Итзи должен найти безопасный путь через сложный лабиринт запутанной паутины, решая задачи, связанные с нахождением различных углов. Вашей конечной целью является найти  для Итзи безопасный путь к вратам искривления времени, уничтожая по дороге синих птиц и решая геометрические проблемы. 

    Обратите внимание, что вы не можете управлять движением Итзи непосредственно. Вы только поворачиваете маховик старых часов, а все остальное движение происходит под действием силы тяжести. Если вы правильно решаете геометрические задачи, то кликая по прямым можете в нужный момент убирать их, освобождая путь для движения или, наоборот, закрывать его.

   Чтобы Итзи не упал и не разбился, вам придется вспомнить теоремы об углах при параллельных прямых прямых, углах в треугольнике и многое другое. 

Попробуйте, это очень интересно!

Как найти третий угол в треугольнике.

     Во многих задачах требуется найти один из углов треугольника. Разберемся, как это можно сделать, рассмотрев наиболее часто встречающиеся случаи.

 Как найти третий угол, если известны два других угла.

     Если вам известны значения двух углов треугольника, то найти третий угол не составит большого труда. Просто надо вспомнить, теорему о внутренних углах треугольника и вычесть сумму двух известных углов из 180°.

     Например, пусть нам известно, что один из углов треугольника равен 70°, а второй 43°.Найдем третий угол.

     Так как сумма углов треугольника всегда равна 180°, то первое, что нам нужно сделать - это найти сумму двух известных углов: 70° + 43° = 113°, и второе, вычесть полученный результат из 180°: 180° - 113° = 67°. Теперь мы знаем третий угол треугольника. 

     Проверить, что задача решена правильно, можно сложив все три угла, и убедиться, что полученная сумма равна 180°: 70° + 43° + 67° = 180°.

     Поработайте с тренажером, и убедитесь, что находить неизвестный угол в этом случае очень просто.

   

Как найти третий угол в равнобедренном треугольнике

     Равнобедренные треугольники имеют две равные стороны и два равных угла, прилежащих к этим сторонам. Если вы знаете один из равных углов в равнобедренном треугольнике, то вы можете найти и два других угла. Вот как это сделать: 

     Пусть известен один из углов при основании равнобедренного треугольника.  Но поскольку, углы при основании равны, значит известен и второй угол. А дальше поступаем по разобранному выше алгоритму: Складываем эти два угла и вычитаем полученную сумму из 180°.

     А теперь, пусть  угол при вершине равнобедренного треугольника равен 30°. В этом случае будем действовать таким образом:

    Вначале вычтем из 180° данный угол. 180° - 30° = 150°. Так мы найдем сумму двух других углов. А поскольку углы при основании равнобедренного треугольника равны, то чтобы найти каждый из углов, нужно полученную сумму разделить на два: 150° : 2 = 75°.

Попробуем найти третий угол в равнобедренном треугольнике на практике

Как найти третий угол в прямоугольном треугольнике

     Например, дан прямоугольный треугольник, в котором один из углов равен 27°. Если это прямоугольный треугольник, то один из его углов равен 90°. Все, что вам нужно сделать, это сложить известные углы (27° + 90° = 117°) и вычесть эту сумму из 180°, то есть 180° - 117° = 63°. Третий угол равен 63°.
     Можно поступить проще. Так как сумма всех углов в треугольнике равна 180°, то на два острых угла в прямоугольном треугольнике остается всегда 90°. Поэтому, чтобы найти третий угол прямоугольного треугольника, достаточно из 90° вычесть известный угол. 90° - 27° = 63°. Как видим, результат один и тот же.

Теперь можете поработать с новыми тренажерами и закрепить полученные знания,

    

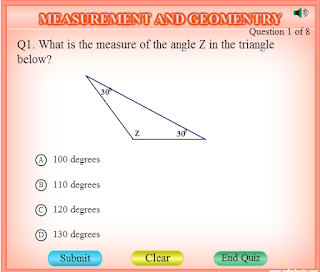
Найдите третий угол треугольника

Найдите третий угол треугольника

     или выполнить тест

Тренажеры сложения десятичных дробей

           
     Предлагаю вам несколько различных тренажеров.  Выбирайте любой и совершенствуйте свои навыки сложения десятичных дробей.
    В первом и втором можно настраивать уровень сложности. Начинайте с простых заданий, а затем переходите к более сложным.
     В третьем тренажере, из открывшегося меню выберите пункт "Add 1/10-ths"
     Помните, что все тренажеры англоязычные, поэтому разделителем дробной части служит точка, а не запятая, как мы привыкли.

Умножение и деление десятичных дробей на 0,1, 0,01, 0,001

     Довольно часто приходится умножать десятичные дроби на 0,1, 0,01, 0,001 и так далее. Поэтому целесообразно сформулировать правило умножения десятичной дроби на эти числа. 

Поскольку 0,1 = 1/10, 0,01 = 1/100 0,001 = 1/1000, то умножение на 0,1 0,01, 0,001 и т.д. равносильно делению на 10, 100, 1000 и т.д., которые мы уже разобрали здесь.

    Поэтому, умножение данной десятичной дроби на 0,1, 0,01, 0,001 и так далее дает дробь, которая получается из исходной, если в ее записи перенести запятую влево на 1, 2, 3 и так далее цифр соответственно, при этом если цифр для переноса запятой не хватает, то нужно слева дописать необходимое количество нулей.

     Например, чтобы умножить десятичную дробь 54,34 на 0,1, надо в дроби 54,34 перенести запятую влево на 1 цифру, при этом получится дробь 5,434, то есть, 54,34 · 0,1 = 5,434. 

    Приведем еще один пример. Умножим десятичную дробь 9,3 на 0,0001. Для этого нам нужно в умножаемой десятичной дроби 9,3 перенести запятую на 4 цифры влево, но запись дроби 9,3 не содержит такого количества знаков. Поэтому нам нужно в записи дроби 9,3 слева приписать столько нулей, чтобы можно было беспрепятственно осуществить перенос запятой на 4 цифры, следовательно, будем иметь 9,3 · 0,0001 = 0,00093

      Ниже вы можете посмотреть динамические модели умножения 

    

Попробуйте выполнить задания

Для выполнения этого задания вам потребуются не только знания, но и отличная реакция

     

Теперь разберемся с делением. 

     Аналогично, так как 0,1=1/10, 0,01=1/100 и т.д., то из правила деления на обыкновенную дробь следует, что разделить десятичную дробь на 0,1, 0,01, 0,001 и т.д. это все равно, что умножить данную десятичную дробь на 10, 100, 1000 и т.д. соответственно.

     Вспоминаем соответствующее правило и приходим к выводу, что чтобы разделить десятичную дробь на 0,1, 0,01, 0,001… нужно перенести запятую вправо на 1, 2, 3, … цифры, при этом если цифр в записи десятичной дроби недостаточно для переноса запятой, то справа нужно дописать необходимое количество нулей.

     Например, 5,739 : 0,1=57,39;  0,21 : 0,00001=21 000.

       Чтобы не ошибаться в умножении и делении нужно понять или хотя-бы запомнить следующее:
     при умножении на число большее единицы десятичная дробь увеличивается и ее запятая передвигается вправо;
     при умножении на число меньшее единицы десятичная дробь уменьшается и ее запятая передвигается влево;

     при делении на число большее единицы десятичная дробь уменьшается и ее запятая передвигается влево;

     при делении на число меньшее единицы десятичная дробь увеличивается и ее запятая передвигается вправо;

       Во всех случаях запятая передвигается на столько разрядов, сколько нулей в числе на которое мы умножаем или делим.

     Попробуйте применить полученные знания, решая примеры, работая с тренажерами.

Деление на разрядные единицы

    А теперь попробуем не запутаться, выполняя и деление и умножение. Называйте ответ, а потом проверяйте себя

    Если нажать на кнопку "Back", то можно в меню "Play" выбрать этот тренажер в виде игры,